# 哈希
# 1 两数之和
思路:二分查找。不过要注意下标,采用下标索引转换。
public int[] twoSum(int[] nums, int target) { | |
int n = nums.length; | |
Integer[] indices = new Integer[n]; | |
for (int i = 0; i < n; i++) { | |
indices[i] = i; | |
} | |
Arrays.sort(indices, Comparator.comparingInt(a -> nums[a])); | |
for (int i = 0; i < n; i++) { | |
int need = target - nums[indices[i]]; | |
int index = binarySearch(nums, need, indices, i + 1, n - 1); | |
if (index != -1) { | |
return new int[]{indices[i], index}; | |
} | |
} | |
return new int[]{}; | |
} | |
public int binarySearch(int[] nums, int target, Integer[] indices, int left, int right) { | |
while (left <= right) { | |
int mid = left + (right - left) / 2; | |
int midValue = nums[indices[mid]]; | |
if (midValue == target) { | |
return indices[mid]; | |
} else if (midValue < target) { | |
left = mid + 1; | |
} else { | |
right = mid - 1; | |
} | |
} | |
return -1; | |
} |
- 学习
Arrays.sort(indices, Comparator.comparingInt(a -> nums[a])); - 学习
indices索引
# 49 字母异位词分组
关键点:排序,哈希表
class Solution { | |
public List<List<String>> groupAnagrams(String[] strs) { | |
Map<String, List<String>> map = new HashMap<String, List<String>>(); | |
for (String str : strs) { | |
char[] array = str.toCharArray(); | |
Arrays.sort(array); | |
String key = new String(array); | |
List<String> list = map.getOrDefault(key, new ArrayList<String>()); | |
list.add(str); | |
map.put(key, list); | |
} | |
return new ArrayList<List<String>>(map.values()); | |
} | |
} |
# 128 最长连续数列
有几个关键点:
- 第二次遍历的时候是遍历哈希表。为什么呢?因为哈希表可以去重,如果数组是 10^9 个 1,那么哈希表内只有一个 1 ,大大减少时间。
- 为了降低时间复杂度,依据特性,需要判断
!set.contains(num - 1),从而把时间复杂度从 降为
class Solution { | |
public int longestConsecutive(int[] nums) { | |
HashSet<Integer> set = new HashSet<Integer>(); | |
for (int num: nums) { | |
set.add(num); | |
} | |
int longestStreak = 0; | |
for (int num : set) { | |
if (!set.contains(num - 1)) { | |
int currentNum = num; | |
int currentStreak = 1; | |
while (set.contains(currentNum + 1)) { | |
currentNum += 1; | |
currentStreak += 1; | |
} | |
longestStreak = Math.max(longestStreak, currentStreak); | |
} | |
} | |
return longestStreak; | |
} | |
} |
# 双指针
# 283 移动零
两个方法,一个是双指针(即维护两个下标),一个是原地栈
# 双指针
使用双指针,左指针指向当前已经处理好的序列的尾部(实际上不是尾部,是尾部后的第一个不在该序列内的数字),右指针指向待处理序列的头部。
右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。
class Solution { | |
public void moveZeroes(int[] nums) { | |
int n = nums.length, left = 0, right = 0; | |
while (right < n) { | |
if (nums[right] != 0) { | |
swap(nums, left, right); | |
left++; | |
} | |
right++; | |
} | |
} | |
public void swap(int[] nums, int left, int right) { | |
int temp = nums[left]; | |
nums[left] = nums[right]; | |
nums[right] = temp; | |
} | |
} |
# 原地栈
原理就是第一次遍历获得 0 的个数并删去 0,第二次把 0 加上去。但是这里精妙点就在于把获得 0 的个数与删去 0 两件事合在同一次循环里完成了。
由于 i 必定大于等于 j,利用特性可以在该次循环中就进行覆盖去除 0,不会导致非 0 值被意外覆盖的情况。这个做法个人认为是相当巧妙且比上面那个好懂的。
public void moveZeroes(int[] nums) { | |
int j = 0; | |
for (int i = 0; i < nums.length; i++) { | |
if (nums[i] != 0) { | |
nums[j] = nums[i]; | |
j++; | |
} | |
} | |
while (j < nums.length) { | |
nums[j] = 0; | |
j++; | |
} | |
} |
# 11 盛最多水的容器
感觉之前就做过这个题。思路是双指针指向最左与最右(下标),依次移动其中较小的一个,直到二者重合。
那么为什么是移动较小的那个呢?因为我们的目的是找到最大的,但是我们不知道最大的在哪,那么我们的移动其实是有随机性的。但是我们可以证明,如果不移动较小的那方而是移动较大的那方,后面的容量是肯定比一开始的小的。这个可以画图直观感受。
所以,因为随机性的存在我们需要尝试,那就只能移动较大的那一方的。依次移动,每次记录值并且更新最大值,直到重合所有情况列举完毕。
换言之,就是一个怎么做到最大收益移动的问题。因为移动的方式只有两种,有一种可以肯定只会越来越差,那么就选取另一个了。
public int maxArea(int[] height) { | |
int max = 0; | |
int left = 0; | |
int right = height.length - 1; | |
while (left < right) { | |
int area = Math.min(height[left], height[right]) * (right - left); | |
max = Math.max(max, area); | |
if (height[left] < height[right]) { | |
left++; | |
} else { | |
right--; | |
} | |
} | |
return max; | |
} |
# 15 三数之和
先排序,再三层循环,保证枚举出的 a <= b <= c,优化不重复枚举,其中 c 从右向左遍历。
但是这题巧妙的点还挺多的,关键在于如何最大化利用升序数组这个性质,从而实现多指针的最少数量遍历。
这个是我大概看了题解思路后写的第一版代码,不过超时了:
public List<List<Integer>> threeSum(int[] nums) { | |
List<List<Integer>> result = new ArrayList<>(); | |
Arrays.sort(nums); | |
for (int i = 0; i < nums.length - 2; i++) { | |
if (i > 0 && nums[i] == nums[i - 1]) { | |
continue; | |
} | |
int target = -nums[i]; | |
for (int j = i + 1; j < nums.length - 1; j++) { | |
if (j > i + 1 && nums[j] == nums[j - 1]) { | |
continue; | |
} | |
int right = nums.length - 1; // 注意点 1 | |
while (j < right) { | |
if (nums[j] + nums[right] > target) { // 巧妙点 | |
right--; | |
} else { | |
break; | |
} | |
} | |
if (j == right || nums[j] + nums[right] != target) { | |
continue; // 注意点 2 | |
} | |
List<Integer> triplet = new ArrayList<>(); | |
triplet.add(nums[i]); | |
triplet.add(nums[j]); | |
triplet.add(nums[right]); | |
result.add(triplet); | |
} | |
} | |
return result; | |
} |
巧妙点这一行,先想,我们需要找到的是 nums[j] + nums[right] == target 的情况,而我们已经将数组事先排序,那么当 j 固定而 right 逐渐向左逼近的过程中, nums[j] + nums[right] 肯定是越来越小的,而如果某一点 right 的值已经使和小于 target 了,那么再逼近也没有意义了,所以可以退出第三层循环。
但是,在我写的代码里面,right 是每次二层循环重定义一次的,这导致耗时还是很久。下面的是优化后的:
public List<List<Integer>> threeSum(int[] nums) { | |
List<List<Integer>> result = new ArrayList<>(); | |
Arrays.sort(nums); | |
for (int i = 0; i < nums.length - 2; i++) { | |
if (i > 0 && nums[i] == nums[i - 1]) { | |
continue; | |
} | |
int target = -nums[i]; | |
int right = nums.length - 1; // 对应注意点 1 | |
for (int j = i + 1; j < nums.length - 1; j++) { | |
if (j > i + 1 && nums[j] == nums[j - 1]) { | |
continue; | |
} | |
while (j < right) { | |
if (nums[j] + nums[right] > target) { | |
right--; | |
} else { | |
break; | |
} | |
} | |
if (j == right) { | |
break; // 对应注意点 2 | |
} | |
if (nums[j] + nums[right] == target) { | |
List<Integer> triplet = new ArrayList<>(); | |
triplet.add(nums[i]); | |
triplet.add(nums[j]); | |
triplet.add(nums[right]); | |
result.add(triplet); | |
} | |
} | |
} | |
return result; | |
} |
这里,我们对二层循环也进行了优化。思考一下,为什么 right 可以在第一层循环就定义?而对应的为什么当 j == right 后,我们就可以退出第二层循环了?
先解释第二个问题。还是那个道理,我们的目的是逼近 j 和 right,找到 nums[j] + nums[right] == target 的情况。我们可以看到,当 j == right 时,那必然第三层循环全部进行完毕,也就是对于固定的 j,所有的 right 全都使 nums[j] + nums[right] > target ,在这个时候,继续逼近 j 也就是增大 j 的值,那么其和必然还是大于 target 的,所以完全可以退出第二层循环了。
我们优化完这一点后已经可以通过测试,但是耗时还是很久。接下来就是第一个问题 —— 为什么 right 可以在第一层循环就定义?这个换句话说就是,为什么 right 的值在第二层循环是可以继承复用的。
我们还是从目的讲起,逼近 j 和 right,找到 nums[j] + nums[right] == target 。那么,介于上面我们知道除去到达终点外退出第二层循环的条件是 j == right ,所有的 j 和 right 全都使 nums[j] + nums[right] > target ,那么,继续进行第二层循环即代表着存在一个 right, nums[j] + nums[right] <= target (当然,等于的情况已经被加入结果中了),而 right + 1(如果存在的话),它可以使和大于 target。那么现在,我们需要逼近 j,从而试图找到能让和等于 target 的值。
我们现在举例几个下标 1 2 3 4 5 6. 假设 j == 1,right == 5, nums[1] + nums[6] > target ,而 nums[1] + nums[5] < target ,再向右逼近 right 已经没有意义,只能向左逼近 j。那么为什么 right 可以复用呢?我们假设 j 逼近到 2,right 还是重新从 6 开始计算, nums[2] + nums[6] 必然大于 nums[1] + nums[6] 也必然大于 target,所以是可以复用的。
这题可以说是优化的相当精妙了,佩服佩服。个人认为,还是得找到核心目的,从目的出发,一步步优化方法实现,利益最大化。
# 42 接雨水
官方给了三种题解:动态规划、栈与双指针,个人觉得栈那个方法有点反人类直觉了。
# 动态规划

看这张直观图,可以看到,低洼处可以积水,积水高度与两边最矮的高度直接相关。是不是有点像盛最多水的容器这题?
那么,我们现在只考虑一个单位长度的地方能否积水(也就是能否形成一个长条)。这个需要符合什么条件呢?答案是该点处左右两点的高度都需要大于它。
那么,在该点处的积水量(也就是长条高度),由什么决定呢?我们假设这么一个数组: [1, 2, 1, 0, 1, 1, 3, 2] ,考虑在高度为 0 处的积水量,从该点先往左看,找到其非递减的最高高度,那就是 2;再向右看,找到非递减的最高高度,那就是 3。最后,取这两者的最小值,再减去自身的高度,得到的就是在这一点的积水量了。这个可以意会一下。
理论成立,现在落实到算法上。我们可以先通过两轮遍历,获得每点左边及右边符合上面理论的值。我们会发现找这个值是很容易的。

找到值后直接遍历数组,先判断能否积水,再算出积水值总和即可。
public int trap(int[] height) { | |
int sum = 0; | |
int[] leftMax = new int[height.length]; | |
int[] rightMax = new int[height.length]; | |
leftMax[0] = height[0]; | |
rightMax[height.length - 1] = height[height.length - 1]; | |
for (int i = 1; i < height.length; i++) { | |
leftMax[i] = Math.max(leftMax[i - 1], height[i]); | |
} | |
for (int i = height.length - 2; i >= 0; i--) { | |
rightMax[i] = Math.max(rightMax[i + 1], height[i]); | |
} | |
for (int i = 0; i < height.length; i++) { | |
if (Math.min(leftMax[i], rightMax[i]) - height[i] > 0) { | |
sum += Math.min(leftMax[i], rightMax[i]) - height[i]; | |
} | |
} | |
return sum; | |
} |
# 双指针法
和上面那个用的是同一个理论。就是可能没那么直观了。
public int trap(int[] height) { | |
int sum = 0; | |
int left = 0; | |
int right = height.length - 1; | |
int leftMax = 0; | |
int rightMax = 0; | |
while (left < right) { | |
leftMax = Math.max(leftMax, height[left]); | |
rightMax = Math.max(rightMax, height[right]); | |
if (height[left] < height[right]) { | |
sum += leftMax - height[left]; | |
left++; | |
} else { | |
sum += rightMax - height[right]; | |
right--; | |
} | |
} | |
return sum; | |
} |
# 滑动窗口
# 3 无重复字符的最长子串
整体思路是遍历所有子串,判断它是否无重复字符,更新最大值。
最暴力情况下,时间复杂度为 ,那么,我们重点就是要优化这个遍历过程,尽量减少遍历次数。
left 左指针,right 右指针,首先固定左指针向右遍历,当检测到某个右指针子串有重复时,立即退出内循环,更新外循环。有一个很明显的优化思路:我们一次遍历下来的结果,是否可以保留中间已经判断过无重复的部分,留给下一次遍历呢?
public int lengthOfLongestSubstring(String s) { | |
int max = 0; | |
char[] chars = s.toCharArray(); | |
int right = -1; | |
HashSet<Character> set = new HashSet<>(); | |
for (int left = 0; left < s.length(); left++) { | |
if (left > 0) { | |
set.remove(chars[left - 1]); | |
} | |
while (right + 1 < s.length() && !set.contains(chars[right + 1])) { | |
set.add(chars[right + 1]); | |
right++; | |
} | |
max = Math.max(max, right - left + 1); | |
if (right == s.length() - 1) { | |
break; | |
} | |
} | |
return max; | |
} |
本质上我们这里做的是 right 的复用,right 停在检测到的最后一个符合当前子串为无重复子串的位置上,在下一轮继续判断 set.contains(chars[right + 1]) 成立与否。
或许也可以花一点功夫,把 left 移到最合适的位置上(比如 "aebcdbacd",aebcd 判断后遇见第一个重复的 b,right 停留在 d 上,将 left 并非向前一步移到 e 而是直接移到 c 上)。但是我觉得花的这个功夫耗的时间也不能优化多少整体。
# 438 找到字符串中的所有字母异位词
public List<Integer> findAnagrams(String s, String p) { | |
int sLength = s.length(); | |
int pLength = p.length(); | |
if (sLength < pLength) { | |
return new ArrayList<>(); | |
} | |
List<Integer> result = new ArrayList<>(); | |
int[] pCount = new int[26]; | |
int[] sCount = new int[26]; | |
for (int i = 0; i < pLength; i++) { | |
pCount[p.charAt(i) - 'a']++; | |
sCount[s.charAt(i) - 'a']++; | |
} | |
if (Arrays.equals(pCount, sCount)) { | |
result.add(0); | |
} | |
for (int i = 0; i < sLength - pLength; i++) { | |
sCount[s.charAt(i) - 'a']--; | |
sCount[s.charAt(i + pLength) - 'a']++; | |
if (Arrays.equals(pCount, sCount)) { | |
result.add(i + 1); | |
} | |
} | |
return result; | |
} |
这题比较简单,滑动窗口思想,固定长度窗口依次遍历,同时,保留能够复用的部分,每次只要去除无用部分并加上新增部分即可。
# 子串
# 560 和为 K 的子数组
前缀和思路,非常巧妙的一题!!!
本题要求的是子数组和为 K 的数目,因为是连续子数组,刚刚又做了滑动窗口那几题,很明显就会想成窗口遍历的思路了。但是这个思路再怎么优化时间复杂度也是 。那么,我们能不能换个角度呢?
形象化,我们要求 [i, j] 范围数组的和,那么,我们是不是可以转化一下: Sum[i, j] = Sum[0, j] - Sum[0, i - 1] 。 Sum[0, i] ,不就是前缀和嘛。
通过计算出所有的前缀和,我们就能得到任意 Sum[i, j] 的值。但是这还不行啊,这不还得遍历所有 i j 可能性求值判断吗。这个时候,哈希表就来了。
public int subarraySum(int[] nums, int k) { | |
int count = 0; | |
HashMap<Integer, Integer> map = new HashMap<>(); | |
int sum = 0; | |
map.put(0, 1); // 必须要加 | |
for (int i = 0; i < nums.length; i++) { | |
sum += nums[i]; | |
if (map.containsKey(sum - k)) { | |
count += map.get(sum - k); | |
} | |
map.put(sum, map.getOrDefault(sum, 0) + 1); // 必须要放在后面 | |
} | |
return count; | |
} |
可以看到,我们哈希表的键值反而是 sum ,后面 value 则是对应出现的次数。这是怎么一回事呢?毕竟,我们要得到的只是和为 K 的子数组的数目啊!假设,K 为 10,前缀和为 11 的数组有 2 个,前缀和为 1 的数组有 2 个,那么,我们这里可以得到几个和为 10 的数组呢?很明显,是 4 个。
所以,我们可以直接无视位置,存储其出现次数即可。依次从前往后遍历,获得当前前缀和,先不急着存进去,看对应的 sum - k 有多少个,在 count 中加上本次数就行。
为什么加完后再存呢,主要是防止 sum - k = sum 也就是 k 为 0 的情况。如果放在前面,就会出现空数组,而本题对于子数组定义是非空的,因此不符合题干。此外也要注意在循环之前我们加上了 map.put(0, 1); ,也就是前缀和为 0 的天生有一个空数组情况,这个与结果的子数组是区分开的。可以自己试一下体会一下这两个分别起了什么作用。
# 239 滑动窗口最大值
这一题咋一看感觉还挺简单的,固定窗口移动,给出每个窗口内的最大值。那么,也完全可以像前几题一样,沿用已比较值复用的思路嘛!所以按照这个思路写了个代码,第一轮(0~k)筛出最大值和第二大的值,然后移动窗口,根据最新加入的值以及离开窗口的值,依次更新这两个。然后问题就来了 —— 万一最大值和第二大的值在后面都因为离开窗口没了怎么办呢!
但是这个总体思路肯定是没错的,就是这里我们究竟要记录上个窗口的多少信息复用于下个窗口。
我们看这个数组: [1, 2, 5, 4, 3, 6, 1] , k = 4 。现在,假设我们先对下标 0 到 3 进行第一轮获得最大值,很明显是 5,对吧?我们把它记录下来。那么,其他三个也就是 1 2 4,这三个数字要不要记录呢?我们考虑窗口移动的逻辑,最左边的数字会被移出去,那么,在这个数组里,当下标为 2 (即 5)的数字处在窗口中时,下标为 0 和 1 的数字必然不可能在后面的移动中成为最大值,所以我们可以直接排除掉它们。但是对于下标为 3 也就是 4,因为后面 5 会离开窗口,所以我们还是得记录下 4。
“当滑动窗口向右移动时,只要 i 还在窗口中,那么 j 一定也还在窗口中,这是 i 在 j 的左侧所保证的。因此,由于 nums [j] 的存在,nums [i] 一定不会是滑动窗口中的最大值了,我们可以将 nums [i] 永久地移除。”
以此类推,我们维护一个队列,存的是下标,这些下标按从小到大的顺序存储,且其在数组中对应的数字严格递减。总觉得这个想讲完全清楚有点难…… 最好还是要意会一下感受一下。个人觉得还是有些巧妙的。充分地利用了固定窗口滑动的性质,做到了存储所有必要信息用于复用。
public int[] maxSlidingWindow(int[] nums, int k) { | |
int n = nums.length; | |
Deque<Integer> deque = new LinkedList<>(); | |
int[] result = new int[n - k + 1]; | |
for (int i = 0; i < k; i++) { | |
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) { | |
deque.pollLast(); | |
} | |
deque.offerLast(i); | |
} | |
result[0] = nums[deque.peekFirst()]; | |
for (int i = k; i < n; i++) { | |
while (!deque.isEmpty() && nums[deque.peekLast()] <= nums[i]) { | |
deque.pollLast(); | |
} | |
deque.offerLast(i); | |
while (!deque.isEmpty() && deque.peekFirst() <= i - k) { | |
deque.pollFirst(); | |
} | |
result[i - k + 1] = nums[deque.peekFirst()]; | |
} | |
return result; | |
} |
“我悟了, 队尾比不过同龄人的删掉,队头超出时代区间的删掉,历史就是这么不断更迭的。”
—— 出自力扣官方题解评论
# 76 最小覆盖子串
有点难度的一题(毕竟是 Hard)。这一题还是我们滑动窗口,我们先确定大致的思路,再进行优化。
两个指针 left right,首先固定 left 为 0,向右移动 right,当 left 到 right 区段满足题目要求时,我们再固定 right,向右移动 left,尝试找出这一段的最小满足条件区段。找出来后记录长度及坐标,再固定 left,向右移动 right,重复以上过程,找下一组符合题目条件的区间,直到 right 到达最右端。
(下面代码出自灵茶山艾府)
public String minWindow(String S, String t) { | |
int[] cntS = new int[128]; //s 子串字母的出现次数 | |
int[] cntT = new int[128]; //t 中字母的出现次数 | |
for (char c : t.toCharArray()) { | |
cntT[c]++; | |
} | |
char[] s = S.toCharArray(); | |
int m = s.length; | |
int ansLeft = -1; | |
int ansRight = m; | |
int left = 0; | |
for (int right = 0; right < m; right++) { // 移动子串右端点 | |
cntS[s[right]]++; // 右端点字母移入子串 | |
while (isCovered(cntS, cntT)) { // 涵盖 | |
if (right - left < ansRight - ansLeft) { // 找到更短的子串 | |
ansLeft = left; // 记录此时的左右端点 | |
ansRight = right; | |
} | |
cntS[s[left]]--; // 左端点字母移出子串 | |
left++; | |
} | |
} | |
return ansLeft < 0 ? "" : S.substring(ansLeft, ansRight + 1); | |
} | |
private boolean isCovered(int[] cntS, int[] cntT) { | |
for (int i = 'A'; i <= 'Z'; i++) { | |
if (cntS[i] < cntT[i]) { | |
return false; | |
} | |
} | |
for (int i = 'a'; i <= 'z'; i++) { | |
if (cntS[i] < cntT[i]) { | |
return false; | |
} | |
} | |
return true; | |
} |
纯粹按照上面那个思想实现的时间复杂度是 O (∣Σ∣m+n),其中 m 为 s 的长度,n 为 t 的长度,∣Σ∣ 为字符集合的大小,本题字符均为英文字母,所以 ∣Σ∣=52。那么,可以看到每一次判断是否包含都要遍历 26 个字符,那么能不能优化呢?
优化后的代码:
public String minWindow(String S, String t) { | |
if (S == null || t == null || S.length() < t.length()) { | |
return ""; | |
} | |
int[] tCount = new int[128]; | |
for (char c : t.toCharArray()) { | |
tCount[c]++; | |
} | |
int required = t.length(); | |
int left = 0, right = 0, minLength = Integer.MAX_VALUE, start = 0; | |
while (right < S.length()) { | |
char cRight = S.charAt(right); | |
if (tCount[cRight] > 0) { | |
required--; | |
} | |
tCount[cRight]--; | |
right++; | |
while (required == 0) { | |
if (right - left < minLength) { | |
minLength = right - left; | |
start = left; | |
} | |
char cLeft = S.charAt(left); | |
tCount[cLeft]++; | |
if (tCount[cLeft] > 0) { | |
required++; | |
} | |
left++; | |
} | |
} | |
return minLength == Integer.MAX_VALUE ? "" : S.substring(start, start + minLength); | |
} |
这个主要是复用 tCount[] 以及引入了 required 这个量,从而快速判断是否存在包含关系。很好理解 required 即 t 所需的字母总数,当 required 为 0 时就可以快速判断出包含条件成立。 required 的增减需要实现判断 tCount[i] 是否大于 0,防止误增减。此外对于 tCount[i] 也有动态的增减过程。
# 普通数组
# 53 最大子数组和
比较简单的一题。有贪心与动态规划两个常见的方法,不过受到 560 和为 K 的子数组 这一题的启发,我用的是前缀和的方法,也是拿下了执行时间击败 100%。
public int maxSubArray(int[] nums) { | |
int length = nums.length; | |
int min = 0; | |
int sum = 0; | |
int max = nums[0]; | |
for (int num : nums) { | |
sum += num; | |
max = Math.max(max, sum - min); | |
min = Math.min(min, sum); | |
} | |
return max; | |
} |
计算前缀和,先和当前维护的最小前缀和相减,判断是否最大,再判断是否更新最小前缀和。
为什么不是先判断更新最小前缀和呢?万一本题所有子数组和都小于 0,先更新的话,就会出现空数组导致和为 0 最大的错误情况了。
# 56 合并区间
很简单的一题。感觉重点就是怎么给二维数组排序。
public int[][] merge(int[][] intervals) { | |
int n = intervals.length; | |
Arrays.sort(intervals, (a, b) -> a[0] - b[0]); | |
int[] array_now = intervals[0]; | |
List<int[]> intervals_new = new ArrayList<>(); | |
for (int i = 1; i < n; i++) { | |
if (intervals[i][0] <= array_now[1]) { | |
array_now[1] = Math.max(array_now[1], intervals[i][1]); | |
} else { | |
intervals_new.add(array_now); | |
array_now = intervals[i]; | |
} | |
} | |
intervals_new.add(array_now); | |
return intervals_new.toArray(new int[intervals_new.size()][]); | |
} |
# 189 轮转数组
一开始我的思路挺简单粗暴的:本质上就是把数组后面一段拼接到前面去,直接算出切割位置切分拼接不就好了嘛。然后喜提执行用时击败 3.29%。
后来看了题解,发现一个非常巧妙的方法 —— 既然是要把后面的移到前面去,那我先把整个数组翻转,不就移动了吗?然后,再根据具体 k 值,将两段分别翻转过来,就弄好了。这样也降低了非常多的空间复杂度。
public void rotate(int[] nums, int k) { | |
k %= nums.length; | |
reverse(nums, 0, nums.length - 1); | |
reverse(nums, 0, k - 1); | |
reverse(nums, k, nums.length - 1); | |
} | |
public void reverse(int[] nums, int start, int end) { | |
while (start < end) { | |
int temp = nums[start]; | |
nums[start] = nums[end]; | |
nums[end] = temp; | |
start += 1; | |
end -= 1; | |
} | |
} |
# 238 除自身以外数组的乘积
题目明确写了不能用除法(悲)前缀和 前缀积解法。为了最大化降低空间复杂度,我们先在 answer 数组里记录所有的前缀积。接着,再从后向前遍历 answer ,依次乘上后面的数字。
public int[] productExceptSelf(int[] nums) { | |
int n = nums.length; | |
int[] answer = new int[n]; | |
answer[0] = 1; // 第 0 个数字前面数字的积就视为 1 | |
for (int i = 1; i < n; i++) { | |
answer[i] = answer[i - 1] * nums[i - 1]; | |
} | |
int R = 1; | |
for (int i = n - 1; i >= 0; i--) { | |
answer[i] *= R; | |
R *= nums[i]; | |
} | |
return answer; | |
} |
# 41 缺失的第一个正数
非常抽象的一题。题干要求时间复杂度 ,空间复杂度 ,难度主要就出于此。
主要是利用哈希表的思想,不单独创建一个哈希表,而是将数组视为哈希表。由于特性,我们可以分析得到,最小不存在的正数范围必定为 [1, n+1] 。所以,我们先将所有小于 0 或者大于 n 的数转换成 n+1. 接着,对所有数字进行遍历,下标数对应的正负代表其是否出现过。
public int firstMissingPositive(int[] nums) { | |
int n = nums.length; | |
for (int i = 0; i < n; i++) { | |
if (nums[i] <= 0 || nums[i] > n) { | |
nums[i] = n + 1; | |
} | |
} | |
for (int i = 0; i < n; i++) { | |
int num = Math.abs(nums[i]); | |
if (num > n) { | |
continue; | |
} | |
nums[num - 1] = -Math.abs(nums[num - 1]); | |
} | |
for (int i = 0; i < n; i++) { | |
if (nums[i] > 0) { | |
return i + 1; | |
} | |
} | |
return n + 1; | |
} |
# 矩阵
# 73 矩阵置零
就像我以前说的,为了寻找意义而去寻找意义没有任何意义,那么我也认为为了优化而优化没有任何意义。所以这里就放最原始的两次遍历的解法。
public void setZeroes(int[][] matrix) { | |
int m = matrix.length, n = matrix[0].length; | |
boolean[] row = new boolean[m]; | |
boolean[] col = new boolean[n]; | |
for (int i = 0; i < m; i++) { | |
for (int j = 0; j < n; j++) { | |
if (matrix[i][j] == 0) { | |
row[i] = col[j] = true; | |
} | |
} | |
} | |
for (int i = 0; i < m; i++) { | |
for (int j = 0; j < n; j++) { | |
if (row[i] || col[j]) { | |
matrix[i][j] = 0; | |
} | |
} | |
} | |
} |
# 54 螺旋矩阵
总感觉我什么时候写过这一题……?算了不管了,我是比较喜欢人类一点的做法的,看了大佬的题解受益颇多。
主要就是使用方向矩阵,这个 CPL 老师也讲过。怎么记录已经走过的点呢?第一种方法就是改变原数组,走过的点置最大整数。第二种方法,找规律,比如一个 3 * 4 的矩阵,横向路径走过的路径长是 4_3_2,纵向 2_1,看得出来一个是 n 递减,一个是 m-1 递减。这样就可以清楚每次应该走多少步了。
public List<Integer> spiralOrder(int[][] matrix) { | |
int[][] dirs = <!--swig0-->; | |
int m = matrix.length, n = matrix[0].length; | |
List<Integer> ans = new ArrayList<>(); | |
int i = 0, j = -1; // 注意从 (0, -1) 开始 | |
int size = m * n; | |
m--; | |
for (int di = 0; ans.size() < size; di = (di + 1) % 4) { | |
if (di % 2 == 0) { | |
for (int k = 0; k < n; k++) { | |
j += dirs[di][1]; | |
ans.add(matrix[i][j]); | |
} | |
n--; | |
} else { | |
for (int k = 0; k < m; k++) { | |
i += dirs[di][0]; | |
ans.add(matrix[i][j]); | |
} | |
m--; | |
} | |
} | |
return ans; | |
} |
有一个很巧妙的点,就是 di = (di + 1) % 4 。每次加 1 在方向数组里就相当于转 90°,加到 3 了再加就变回 0。
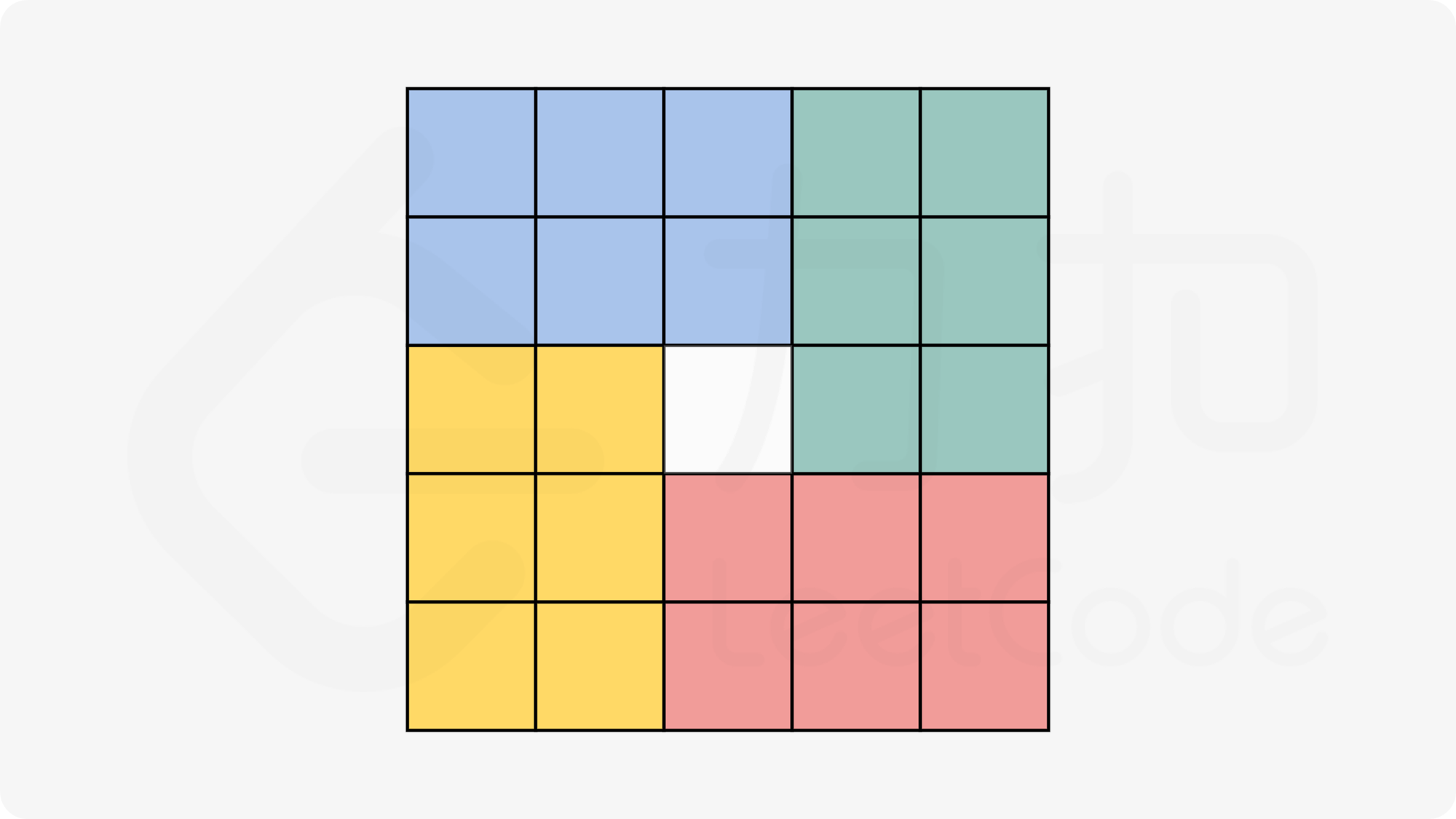
# 48 旋转图像
核心要点:找规律
关键等式:
四个一组旋转,对于整个矩形,只需要截取出四分之一的区域,进行四个一组的轮换即可。下面的四个坐标都是用上面那个等式推出来的。
public void rotate(int[][] matrix) { | |
int n = matrix.length; | |
for (int i = 0; i < n / 2; ++i) { | |
for (int j = 0; j < (n + 1) / 2; ++j) { | |
int temp = matrix[i][j]; | |
matrix[i][j] = matrix[n - j - 1][i]; | |
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]; | |
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]; | |
matrix[j][n - i - 1] = temp; | |
} | |
} | |
} |
# 240 搜索二维矩阵 II
一个特别巧妙的做法,主要还是充分利用了题面性质代码还特别简洁!
题干说:每行的元素从左到右升序排列,每列的元素从上到下升序排列。那么,我们的初始设为从矩阵右上角开始遍历。先明确性质:该处是此行的最大值,也是此列的最小值。
假设我们的目标值是 k,而矩阵右上角值为 n,当 n <k 时,代表了什么?代表这一行所有值都小于 k,那么,我们在接下来的遍历里可以将此行去除。而当 n> k 时,代表了什么?代表这一列所有值都大于 k,那么我们后面可以去除该列。
public boolean searchMatrix(int[][] matrix, int target) { | |
int m = matrix.length; | |
int n = matrix[0].length; | |
int x = 0; | |
int y = n - 1; | |
while (x < m && y >= 0) { | |
if (matrix[x][y] == target) { | |
return true; | |
} | |
if (matrix[x][y] > target) { | |
y--; | |
} else { | |
x++; | |
} | |
} | |
return false; | |
} |
通过更改遍历点坐标的方式简单地实现了上述去除行和列的操作。这个解法真的很清爽……
# 链表
# 106 相交链表
aywc 这不是我们数据结构考试的题目吗()我记得我当时写的是遍历两个链表到尾结点,比较尾结点是不是相同。。不过当时题面应该只是需要给出能不能相交。
来看题,需要找出相交节点。我们设链表 A 非相交部分长度 x,链表 B 非相交部分长度 y,二者相交长度 z。一个等式: (x + z) + y = (y + z) + x 。
假设两个指针 、 分别从两个链表头出发,每次都前进一步,当 到尾部时,让它跳转到链表 B 的头部, 同理。当二者相同时,此时即为链表相交的部分。
public class ListNode { | |
int val; | |
ListNode next; | |
ListNode(int x) { | |
val = x; | |
next = null; | |
} | |
} | |
public ListNode getIntersectionNode(ListNode headA, ListNode headB) { | |
ListNode a = headA; | |
ListNode b = headB; | |
while (a != b) { | |
a = a == null ? headB : a.next; | |
b = b == null ? headA : b.next; | |
} | |
return a; | |
} |
# 206 反转链表
以前做过。
public class ListNode { | |
int val; | |
ListNode next; | |
ListNode(int x) { | |
val = x; | |
next = null; | |
} | |
ListNode(int val, ListNode next) { this.val = val; this.next = next; } | |
ListNode() {} | |
} | |
public ListNode reverseList(ListNode head) { | |
ListNode prev = null; | |
ListNode curr = head; | |
ListNode next = null; | |
while (curr != null) { | |
next = curr.next; | |
curr.next = prev; | |
prev = curr; | |
curr = next; | |
} | |
return prev; | |
} |
简而言之就是记住前中后三个点,将中间点的指向改变即可。
# 234 回文链表
这个需要用到上面那个反转链表。
主要思路,就是找到链表中点,逆转后半部分,将后半部分与前半部分一一对比即可。
public ListNode reverseList(ListNode head) { | |
ListNode prev = null; | |
ListNode curr = head; | |
ListNode next = null; | |
while (curr != null) { | |
next = curr.next; | |
curr.next = prev; | |
prev = curr; | |
curr = next; | |
} | |
return prev; | |
} | |
public boolean isPalindrome(ListNode head) { | |
ListNode slow = head; | |
ListNode fast = head; | |
while (fast != null && fast.next != null) { | |
slow = slow.next; | |
fast = fast.next.next; | |
} | |
// 此时 slow 为链表中点 | |
ListNode secondHalf = reverseList(slow); // 逆转链表后半部分 | |
while (secondHalf != null) { // 注意循环条件 | |
if (head.val != secondHalf.val) { | |
return false; | |
} | |
head = head.next; | |
secondHalf = secondHalf.next; | |
} | |
return true; | |
} |
# 141 环形链表
本题是判断链表是否是环形链表。介于常量内存的要求,我们有两个方法:
一个是标准做法快慢指针。A 指针每次走两步,B 指针每次走一步,若二者相遇则链表有环。
public boolean hasCycle(ListNode head) { | |
if (head == null) { | |
return false; | |
} | |
ListNode slow = head; | |
ListNode fast = head.next; | |
while (fast != null && fast.next != null) { | |
if (slow == fast) { | |
return true; | |
} | |
slow = slow.next; | |
fast = fast.next.next; | |
} | |
return false; | |
} |
一个是有点另类的但是很巧的,即走过一个指针就改变值,如遇到改变的那个值则有环。
public boolean hasCycle(ListNode head) { | |
if (head == null) { | |
return false; | |
} | |
while (head.next != null) { | |
if (head.val == Integer.MAX_VALUE) { | |
return true; | |
} | |
head.val = Integer.MAX_VALUE; | |
head = head.next; | |
} | |
return false; | |
} |
# 142 环形链表 II
上一题的升级版,要求找到入环点,并不允许改变链表内部的值(ban 掉了上面的方法二)。
还是用快慢指针,并且用到了佛洛依德判圈算法。另外这题 CPL 也出过的,不过嘛,CPL 改后的题面导致它有一个更简单的做法了……
public ListNode detectCycle(ListNode head) { | |
ListNode slow = head, fast = head; | |
while (fast != null && fast.next != null) { | |
slow = slow.next; | |
fast = fast.next.next; | |
if (fast == slow) { // 相遇 | |
while (slow != head) { // 再走 a 步 | |
slow = slow.next; | |
head = head.next; | |
} | |
return slow; | |
} | |
} | |
return null; | |
} |
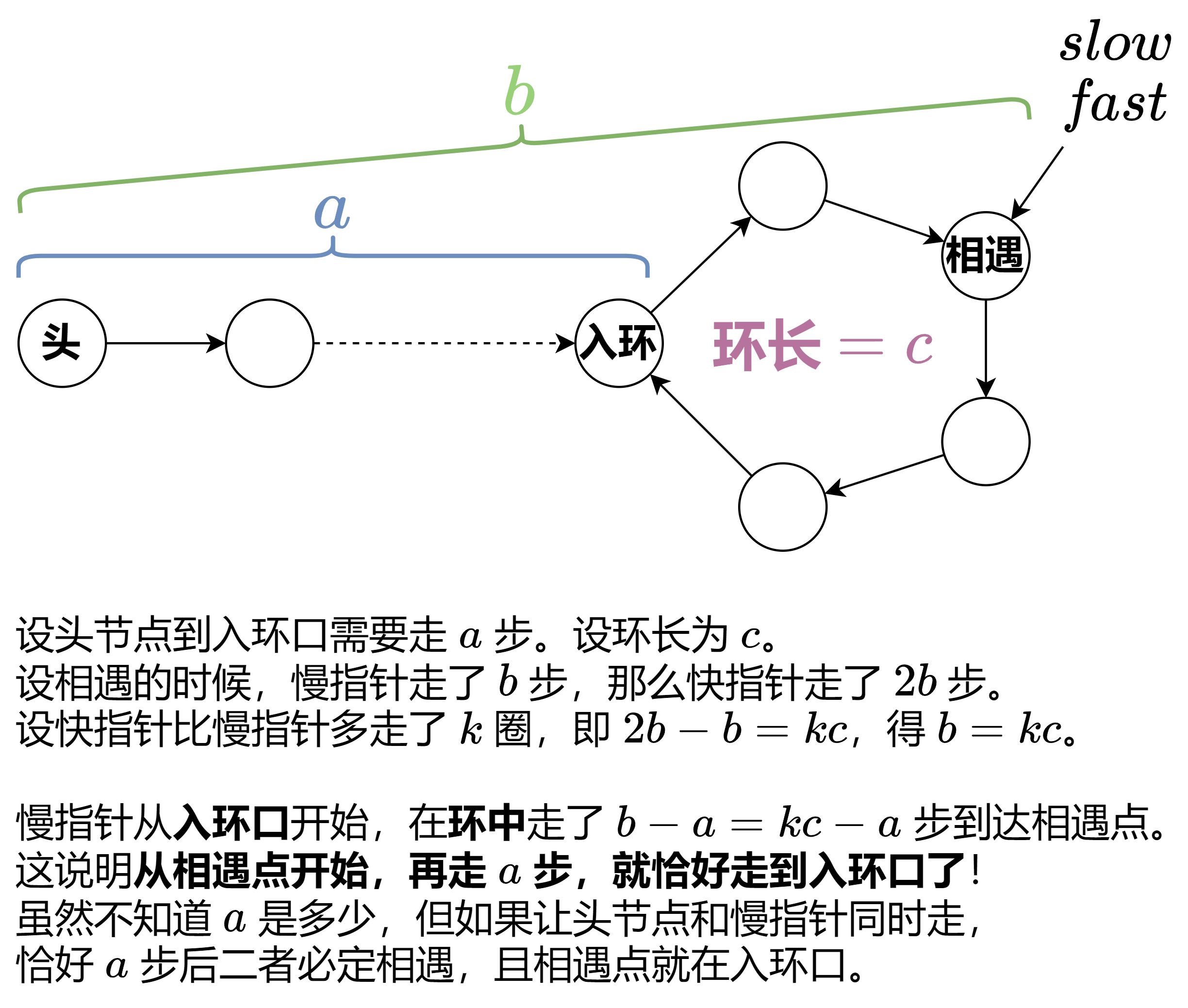
即,根据数学运算得知,快慢指针相遇点的位置距离入环点距离即为 a,即头节点到入环点的距离。
# 2 两数相加
很惊讶于发现这一题我竟然有个去年 5.30 的提交记录,C 语言,12ms 超过了 0% 的人…… 当然,那个时候应该是备战转专业考试来找找手感的。
这一题常规做法就是模拟相加过程。
public ListNode addTwoNumbers(ListNode l1, ListNode l2) { | |
ListNode dummy = new ListNode(-1); | |
ListNode cur = dummy; | |
int carry = 0; | |
while (l1 != null || l2 != null) { | |
int a = l1 == null ? 0 : l1.val; | |
int b = l2 == null ? 0 : l2.val; | |
int sum = a + b + carry; | |
cur.next = new ListNode(sum % 10); | |
cur = cur.next; | |
carry = sum / 10; | |
if (l1 != null) { | |
l1 = l1.next; | |
} | |
if (l2 != null) { | |
l2 = l2.next; | |
} | |
} | |
if (carry != 0) { | |
cur.next = new ListNode(carry); | |
} | |
return dummy.next; | |
} |
持续更新……